Welcome to another note of Poly Notes Hub, here we are discussing about the Different types of Number Systems in Digital Electronics. We are the best platform for diploma or degree engineering notes.
Author Name: Arun Paul.
What is Number System in Digital Electronics?
In digital electronics, a number system is the way of representing and expressing numbers using various symbols (digits). Because digital circuits operate on binary logic (0 and 1), they cannot immediately comprehend the decimal numerals that humans employ.
As a result, digital electronics use many number systems to efficiently represent, process, and store data within electronic devices.
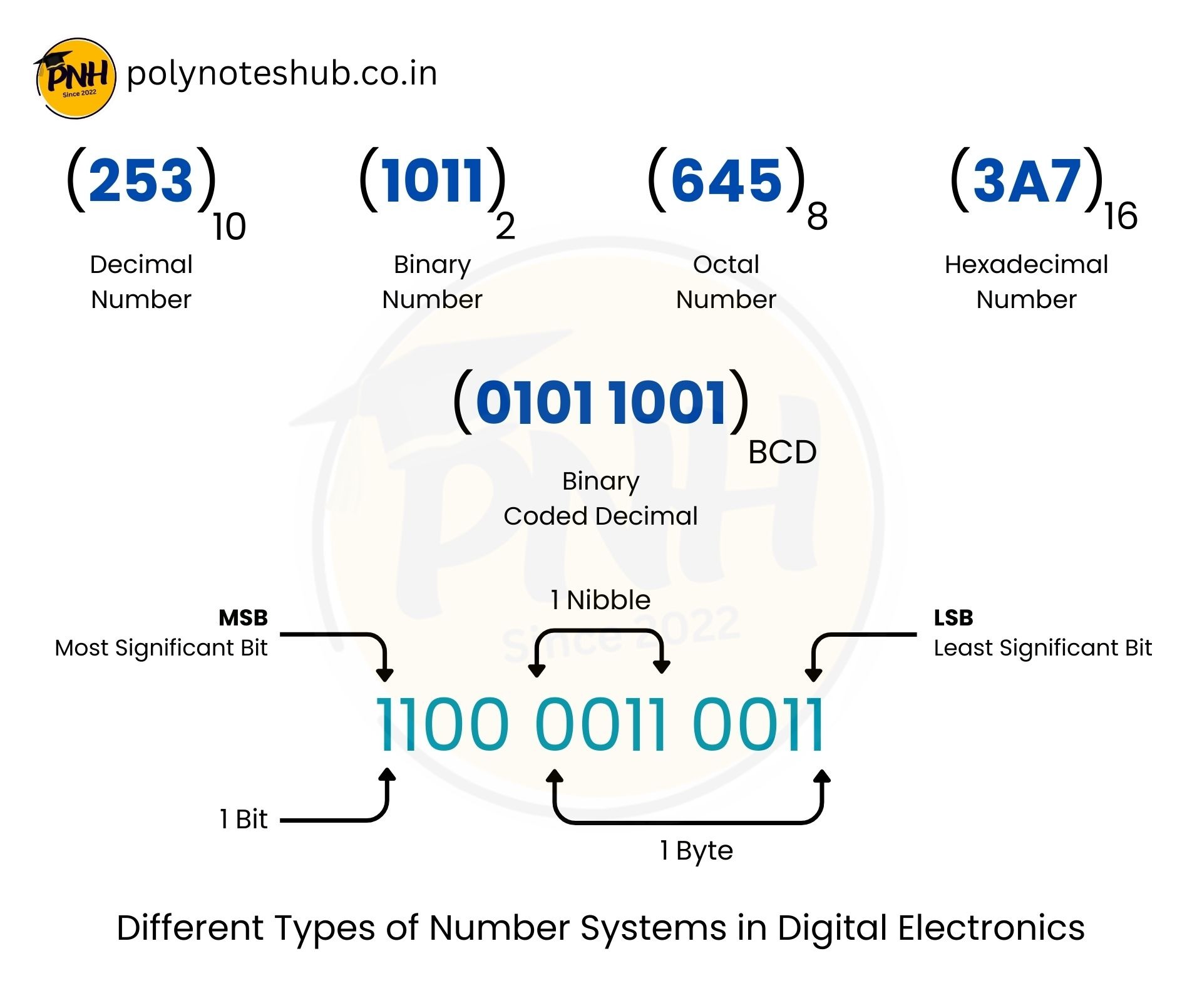
There are various types of number systems in Digital Electronics, which are listed below –
- Decimal (Base-10)
- Binary (Base-2)
- Octal (Base-8)
- Hexadecimal (Base-16)
- BCD (Binary Coded Decimal)
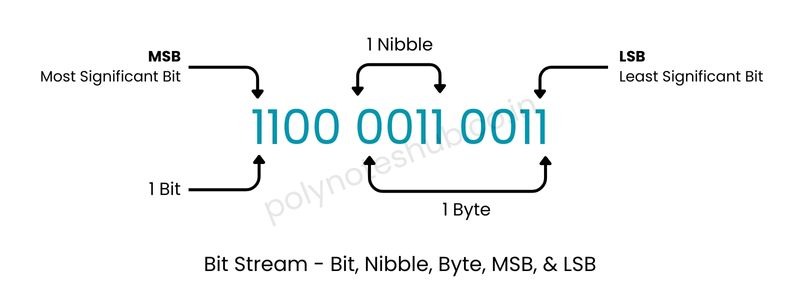
About the Bit Stream and important terms like – Bit, Nibble, Byte, MSB, and LSB
Different Types of Number Systems in Digital Electronics
Here we have listed all the types of number systems definitions with examples –

1. Decimal Number System (Base – 10)
The decimal number system is the most often used positional number system in both daily life and mathematics. It is a base-10 system, which means it is composed of ten unique digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Each digit in a decimal number is assigned a value based on both the digit and its position (place value) in the number. Positional weights in the decimal system are powers of 10, such as 10⁰, 10¹, 10², and so on.
Example:
(253)10 = 2×10² + 5×10¹ + 3×10⁰
2. Binary Number System (Base – 2)
The binary number system is a positional number system that works on base-2, which means it only has two symbols: 0 and 1. These symbols are called bits (binary digits). Binary is the underlying language of digital electronics and computers, as digital circuits have two voltage levels, typically denoted as logic 0 (LOW) and 1 (HIGH). Each point in a binary number indicates a power of 2, such 2⁰, 2¹, 2², and so on.
When a binary number is interpreted, each bit is multiplied by its corresponding power of two, and the results are summed to yield the decimal value.
Example:
(1011)₂ = 1×2³ + 0×2² + 1×2¹ + 1×2⁰
3. Octal Number System (Base – 8)
The octal number system is a positional number system based on base-8, with eight digits (0–7). Each digit in the octal system corresponds to a power of 8 (e.g., 8⁰, 8¹, 8²). Octal was historically essential in early computers because it allowed for a compact representation of binary numbers, with each octal digit corresponding exactly to a group of three binary bits.
This made reading, creating, and debugging machine code considerably easier before contemporary hexadecimal notation took hold.
Example:
(645)₈ = 6×8² + 4×8¹ + 5×8⁰
4. Hexadecimal Number System (Base – 16)
The hexadecimal number system is a positional number system that uses base-16, offering sixteen different symbols:
- 0–9 represent values 0 to 9
- A–F represent values 10 to 15
In hexadecimal numbers, each position represents a power of 16, e.g. 16⁰, 16¹, 16², etc.
Hexadecimal is tremendously significant in computer science, digital electronics, and programming because it provides a highly compact and user-friendly representation of binary integers. One hexadecimal number equals four binary bits (a nibble), making it ideal for encoding memory addresses, machine codes, color values (like in HTML), error codes, and microcontroller instructions.
Example:
(3A7)₁₆ = 3×16² + A×16¹ + 7×16⁰
5. BCD or Binary Coded Decimal Number System
Binary-Coded Decimal (BCD) is a digital encoding method in which each decimal digit (0-9) is represented by a 4-bit binary code. Unlike pure binary representation, which converts a whole number to binary, BCD changes each decimal digit independently.
Example:
Decimal 59
→ 5 = 0101
→ 9 = 1001
So 59 = 0101 1001 (BCD)
Difference Between All of Those Number Systems
Here we have shown the Decimal Number vs Binary Number vs Octal Number Vs Hexadecimal Number Vs BCD Number System –
| Feature | Decimal | Binary | Octal | Hexadecimal | BCD |
|---|---|---|---|---|---|
| Base (Radix) | 10 | 2 | 8 | 16 | Not a base (coding system) |
| Digits / Symbols Used | 0–9 | 0, 1 | 0–7 | 0–9, A–F | 0000–1001 (4-bit codes for 0–9) |
| Common Name | Base-10 | Base-2 | Base-8 | Base-16 | Binary Coded Decimal |
| Used By | Humans | Computers / Digital Circuits | Older computers, shortcuts for binary | Programming, addressing, color codes | Calculators, clocks, meters |
| Bits per Digit | — (not binary) | 1 bit | 3 bits | 4 bits | 4 bits per decimal digit |
| Representation Type | Positional | Positional | Positional | Positional | Digit-wise binary encoding |
| Example | 245 | 101101 | 357₈ | 2F₁₆ | 39 → 0011 1001 |
| Conversion Difficulty | Easy | Medium | Easy (from binary) | Very easy (from binary) | Very easy (digit-by-digit) |
| Main Advantage | Simple to understand | Directly used by hardware | Compact binary representation (3 bits) | Highly compact & readable binary form | Avoids rounding errors, easy display |
| Main Disadvantage | Not used by machines | Long numbers for large values | Less used today | Needs hex knowledge | Occupies more memory than pure binary |
Also, you want to download the notes PDF, then just click on the printer icon below. By a single click, you can easily download the number system notes PDF.